इस ब्लॉग के माध्यम से हम शंकु से संबंधित जानकारी साझा करेंगे, शंकु भी गणित का एक महत्वपूर्ण अध्याय है, क्योंकि शंकु से संबंधित जानकारी आपको 9वीं और 10वीं कक्षा के बच्चों में भी पढ़ने को मिली है, फिर भी आपको Sanku Ka Ayatan को जानने में कठिनाई होती है। इस पोस्ट में आपको Sanku Ka Ayatan और शंकु का सूत्र बताया जाएगा।
शंकु की परिभाषा
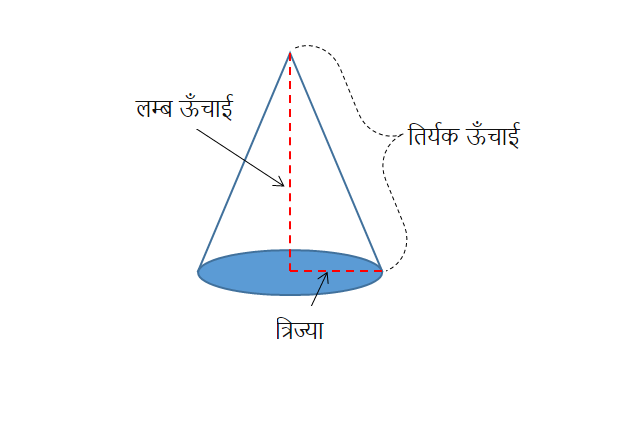
एक समकोण त्रिभुज की भुजा को स्थिर रखकर उसके चारों ओर चक्कर लगाकर निर्मित लंब वृत्तीय शंकु के रूप में जाना जाता है। शीर्ष, आधार, ऊँचाई और तिरछी ऊँचाई शंकु के चार भाग हैं।
Sanku Ka Ayatan
एक शंकु के आयतन की गणना करने के लिए आधार की त्रिज्या और इसकी तिरछी ऊँचाई की मात्रा जानना महत्वपूर्ण है, जिसका एक गोलाकार आधार और एक नुकीला शीर्ष है।
Sanku Ka Ayatan का सूत्र
- शंकु का आयतन =1/3 x πr²h
- शंकु का वक्र पृष्ठ क्षेत्रफल
- शंकु के वक्रपृष्ठ का क्षेत्रफल = πrl
- शंकु का संपूर्ण पृष्ठ का सूत्र
- शंकु के संपूर्ण पृष्ठ का क्षेत्रफल = शंकु का वक्र पृष्ठ का क्षेत्रफल +वृताकार आधार का क्षेत्रफल
= πrl +πr² = πr (l +r)
शंकु के गुणधर्म
- यदि एक शंकु की त्रिज्या को m से बढ़ा दिया जाए, तो Sanku Ka Ayatan m गुणा m² हो जाता है।
- यदि किसी शंकु की ऊंचाई m गुना बढ़ा दी जाए तो Sanku Ka Ayatan भी m गुना हो जाता है।
- यदि शंकु की त्रिज्या m गुनी है और ऊँचाई n गुनी है, तो Sanku Ka Ayatan m²n गुना हो जाता है।
- समान आधार और समान ऊंचाई का एक समवृत्तीय बेलन और एक समवृत्ताकार शंकु, Sanku Ka Ayatan बेलन के आयतन का एक-तिहाई है।
शंकु का फॉर्मूला
- शंकु से संबंधित समस्या को हल करने के लिए आप नीचे दिए गए सूत्र का प्रयोग कर सकते हैं।
- शंकु की तिरछी ऊँचाई ज्ञात करने के लिए, l=⎷r + h
- शंकु के आधार की त्रिज्या ज्ञात करने के लिए, r=⎷l – h
- शंकु की ऊँचाई ज्ञात करने के लिए, h = ⎷l – h
शंकु के छिन्नक के गुण
शंकु के छिन्नक की विशेषताएं इस प्रकार हैं।
- आम धारणा के विपरीत, एक शंकु का छिन्नक वास्तव में शंकु का आधार होता है न कि उसका शीर्ष।
- छिन्नक के दो आधारों के केंद्रों के बीच लंबवत दूरी एक शंकु के छिन्नक की ऊंचाई निर्धारित करती है।
- एक शंकु की ऊँचाई और दो त्रिज्याएँ उसके छिन्नक को निर्धारित करती हैं।
- एक शंकु का छिन्नक भी समवृत्तीय होगा यदि शंकु एक लम्बवृत्तीय शंकु है।
शंकु के छिन्नक का आयतन
- शंकु के छिन्नक का आयतन (V) =π/3 h(R+Rr+r)
- इस सूत्र में, (h) छिन्नक की ऊँचाई है और r छोटे आधार की त्रिज्या है।
- और R बड़े आधार की त्रिज्या है।
- एक शंकु के एक छिन्नक के आयतन की गणना उसकी ऊँचाई और उसके आधारों के क्षेत्रफलों का उपयोग करके की जा सकती है।